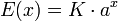funcion exponencial

La función exponencial, es conocida formalmente como la función real e^x, donde e es el número de Euler, aproximadamente 2.71828...; esta función tiene por dominio de definición el conjunto de los números reales, y tiene la particularidad de que su derivada es la misma función. Se denota equivalentemente como f(x)=e^x o exp(x), donde e es la base de los logaritmos naturales y corresponde a la función inversa del logaritmo natural.
En términos mucho más generales, una función real E(x) se dice que es del tipo exponencial en base a si tiene la forma

siendo a, K ∈ R números reales, con a > 0. Así pues, se obtiene un abanico de exponenciales, todas ellas similares, que dependen de la base a que utilicen.

 
 

Teorema (Leyes de los Exponentes) 

Sean a y b reales positivos y x,yΠ ,entonces: 

1.  

2.  

3.  

4.  

5. . 

6 . 

 

Cuando a > 1 ,si x < y, entonces, .Es decir, cuando la base a es mayor que 1,la función exponencial 
de base a es estrictamente creciente en su dominio. 

Cuando 0 < a < 1, si x < y , entonces, . 

Esto significa que la función exponencial de base a < 1 es estrictamente decreciente en 

su dominio. 

. 

10.Si 0< a < b ,se tiene: 

 

. 

Esta propiedad permite comparar funciones exponenciales de diferentes bases. 

11. Cualquiera que sea el número real positivo ,existe un único número realtal que 

. Esta propiedad indica que la función exponencial es sobreyectiva. 

Cuando x e y son enteros, los propiedades enunciadas anteriormente pueden demostrarse usando las definiciones y el teorema 1. Para el caso en el cual x e y son racionales, la demostración utiliza la definición y el teorema 2. Para el caso general, es decir, cuando x e y son reales, la demostración utiliza elementos del análisis real. 
 

Gráfica de la Función Exponencial 

En relación con las propiedades 7 y 8, enunciadas en el teorema, es conveniente hacer algunos comentarios adicionales. 

En primer lugar, en las figuras 1 y 2, aparecen las gráficas de algunas funciones exponenciales de base a > 1 (fig. 1) y de base a < 1 (fig. 2).

fig.1

fig.2

Note que cuando la base aes mayor que 1,la función exponencial (fig.1) no está acotada superiormente. Es decir , crece sin límite al aumentar la variable x. Además, ésta función tiene al cero como extremo inferior. Esto es ,  tiende a cero(0), cuando x toma valores grandes pero negativos. 

Igualmente, cuando la base a< 1, la función exponencial (fig.2) no está acotada superiormente, pero su comportamiento para valores grandes de x, en valor absoluto, es diferente. Así, crece sin límite, al tomar x valores grandes, pero negativos y  tiende a cero, cuando la variable x toma valores grandes positivos. 

El hecho de ser la función exponencial con a> 1, estrictamente creciente (estrictamente decreciente cuando 0 < a< 1), significa que la función exponencial es inyectiva en su dominio.Este hecho y la continuidad de la función son las condiciones que se exigen para garantizar la existencia de la función inversa (función logarítmica), que se presentan en la próxima sección. 

En relación con la propiedad 9, en un sentido, se deduce fácilmente de la definición de función; y, en otro, del hecho de ser la función exponencial inyectiva.