Criterios de existencia de las asintotas horizontales y oblicuas.

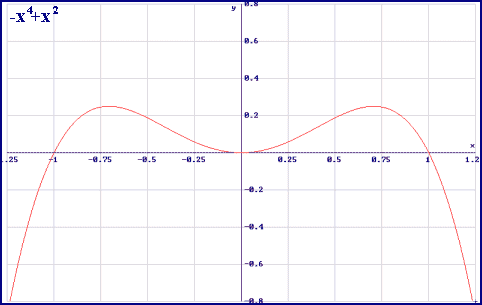
1. Asíntotas horizontales (paralelas al eje OX)
   Si existe el límite: :
   
   
   
   La recta “y = b” es la asíntota horizontal.
   Ejemplo:
    es la asíntota horizontal.
   
   
2. Asíntotas oblicuas (inclinadas)
   Si existen los límites: :
   La recta “y = mx+n” es la asíntota oblicua.
   Ejemplo:
   
    es la asíntota oblicua.

función racional

En matemáticas, una función racional es una función que puede ser expresada de la forma:

donde P y Q son polinomios y x una variable, siendo Q distinto del polinomio nulo. Las funciones racionales están definidas o tienen su dominio de definición en todos los valores de x que no anulen el denominador.¹

La palabra "racional" hace referencia a que la función racional es una razón o cociente (de dos polinomios); los coeficientes de los polinomios pueden ser números racionales o no.

Las funciones racionales tienen diversas aplicaciones en el campo del análisis numérico para interpolar o aproximar los resultados de otras funciones más complejas, ya que son computacionalmente simples de calcular como los polinomios, pero permiten expresar una mayor variedad de comportamientos.

Función racional de grado 2:

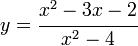Función racional de grado 3:

teorema de factorización

FACTORIZACIÓN DE POLINOMIOS

 

Para factorizar polinomios hay varios métodos:

 

1. Sacar factor común: Es aplicar la propiedad distributiva de la multiplicación respecto de la suma, Así, la propiedad distributiva dice:

 

 

Pues bien, si nos piden factorizar la expresión , basta aplicar la propiedad distributiva y decir que

 

 

Cuando nos piden sacar factor común o simplemente factorizar y hay coeficientes con factores comunes, se saca el máximo común divisor de dichos coeficientes. Por ejemplo, si nos piden factorizar la expresión , será

 

donde 6 es el máximo común divisor de 36, 12 y 18

Para comprobar si la factorización se ha hecho correctamente, basta efectuar la multiplicación, aplicando la propiedad distributiva de la parte derecha de la igualdad, y nos tiene que dar la parte izquierda.

 

Otro ejemplo: Factorizar

 

 ¡Atención a cuando sacamos un sumando completo!, dentro del paréntesis hay que poner un uno. Tener en cuenta que si hubiéramos puesto  y quiero comprobar si está bien, multiplico y me da  pero no  como me tendría que haber dado.

Sin embargo si efectúo

 

Otros ejemplos:

 

 

2. Si se trata de una diferencia de cuadrados: Es igual a suma por diferencia.

Se basa en la siguiente fórmula

 

 

Pero aplicada al revés, o sea que si me dicen que factorice  escribo

 

Otros ejemplos de factorización por este método:

 

 

3. Si se trata de un trinomio cuadrado perfecto: Es igual al cuadrado de un binomio

Se basa en las siguientes fórmulas

 

   y   

 

Así si nos dicen que factoricemos: , basta aplicar la fórmula anterior y escribir que

 

teorema fundamental del algebra

El teorema fundamental del álgebra establece que todo polinomio de una variable no constante con coeficientes complejos tiene un raíz compleja, es decir, existe un número complejo que evaluado en el polinomio da cero. Este incluye polinomios con coeficiente reales, ya que cualquier número real es un número complejo con parte imaginaria igual a cero.

Aunque ésta en principio parece ser una declaración débil, implica todo polinomio de grado n de una variable no constante con coeficientes complejos n tiene, contando con las multiplicidades, exactamente n raíces. La equivalencia de estos dos enunciados se realiza mediante la división polinómica sucesiva por factores lineales.

Hay muchas demostraciones de este importante resultado, que requieren bastantes conocimientos matemáticos para formalizarlas. El nombre del teorema es considerado ahora un error por muchos matemáticos, puesto que es más un teorema del análisis matemático que del álgebra.

teorema del factor y del residuo

Teorema que establece que si un polinomio de x, f(x), se divide entre (x - a), donde a es cualquier número real o complejo, entonces el residuo es f(a).
Por ejemplo, si f(x) = x² + x - 2 se divide entre (x-2), el residuo es f(2) = 2² + (2) - 2 = 4. Este resultado puede volverse obvio si cambiamos el polinomio a una de las siguientes formas equivalentes:
f(x) = (x-2)(x+3) + 4
Como se muestra, la expresión anterior nos puede llevar fácilmente a esperar que 4 sea el residuo cuando f(x) se divide entre (x-2).
El teorema del residuo nos puede ayudar a encontrar los factores de un polinomio. En este ejemplo, f(1) = 1² + (1) - 2 = 0. Por lo tanto, significa que no existe residuo, es decir, (x-1) es un factor. Esto puede mostrarse fácilmente una vez que reacomodamos el polinomio original en una de las siguientes expresiones equivalentes:
f(x) = (x-1)(x+2)
Como se muestra, (x-1) es un factor.

ceros y raices de una función

CORTES CON EJE ABSCISA (x). CEROS DE UNA FUNCIÓN

En el eje de abscisa o eje de coordenadas X, se representan los originales que tienen imagen, es decir, que pertenecen al dominio de F(x). Cuando para un x determinado (x = a) se cumple que F(a) = 0, o lo que es lo mismo, los originales que tienen por imagen al número cero, se dicen que son puntos de corte con el eje abscisa o x. Recuerde que este eje es una recta de ecuación y = 0 (F(x) = 0).   Se dice que x es punto de corte con el eje X si: F(x) = 0. Polinomios.   Se debe, si se puede, factorizar para encontrar los valores que hacen y = P(x) = 0. Raices. P(x) = x3 - 6·x2 + 9·x = x · (x - 3)2 = 0  que se anula para x=0 y x=3 >> P(0)=0 y P(3)=0. Luego hay dos puntos en esta función que están sobre el eje x: (0 , 0) y el (3 , 0).  Racionales.   Es muy común el error, cuando tenemos una expresión del tipo:    n(x)       n(x) numerador C(x) =   ————  = 0        d(x)       d(x) denominador pasar d(x) multiplicando a la derecha de la igualdad, multiplicando al cero y resolver la ecuación n(x) = 0. Si un x = a cumple que n(a) = 0 pero también que d(a) = 0 entonces, x = a,  no es cero de la función C(x). No se verifica que C(a) = 0.   Para que lo sea tiene que cumplirse que n(a) = 0 pero d(a) ≠ 0. Recordar que (0/k)=0 si k ≠ 0.   En un caso práctico, se resuelve n(x) = 0 y las soluciones se sustituye en d(x), excluyendo como ceros aquellos que anulen la función denominador : d(a) = 0.   Vimos que no se puede dividir por cero. Si ese valor anulase el denominador, ese valor no pertenecería al dominio de la función, no pudiendo tener al número cero como imagen. Para que x = a sea punto de corte con el eje x se debe cumplir: C(a) = n(a)/d(a) = 0  »  n(a) = 0 y d(a) ≠ 0 Valores que anulen el numerador y no el denominador Por ejemplo:    (x - 1)·(x - 3)       n(x) numerador C(x) =   ——————  = 0      (x2 - 1)       d(x) denominador x = 1 y x = 3 anulan al numerador, pero sólo x = 3 anula al numerador y no al denominador. Esta función corta al eje x en (3 , 0). El valor x = 1 queda excluido por anular, simultáneamente, al numerador y denominador. Observe como en x = 1 tiene un punto de discontinuidad evitable. No existe C(1). No pertenece al dominio. Exponencial.   Si intentamos resolver F(x) = e-x comprobaremos que e-x ≠ 0 porque e-x > 0 para todo x. Logaritmo. Log f(x) = 0 si     f(x) = 1   ya que Log 1 = 0. Log (x + 2)  ►   x + 2 = 1  ►   x = -1  Log (x2 - 4)  ►   x2 - 4 = 1   ►   x2 = 5  ►    x = ±5(1/2)  (raíz cuadrada de 5). Trigonométrica. sen (x) = 0  si   x = múltiplo de π, es decir  x = k·π   con k entero (Z). cos (x) = 0  si  x = multiplos de π más la mitad de π;   x = (π/2) + k·π  con k entero (Z). tan (x) = 0 donde sen (x) = 0 ya que tan (x) = sen (x) / cos (x). Seno y coseno no se anulan simultáneamente.     Por ejemplo, para la función vista arriba   p(x) = -x4 + x2 = x2·(1 - x2) = 0  ►   x = 0  y  x = ± 1.   Su dominio es R.